

Finaly you need to multiplay it by 2, Because you have 2 sides. $$Iyy = R^4/24 ( 3\theta -3sin\theta -2sin\theta sin^2(\theta/2) $$īased on this equation there is an online calculator which you can plug in first the big segment and find its Iy then the small one and subtract the results to find the I of your section. Similar routine can be applied to find: $Iyy$.Īs mentioned in other answers another way of calculating Ixx is two subtract the I of smaller segment from that of bigger segment. You can search for CG and area of a circle segment. Wolfram has the equation for these " $ y^-$"s, of a segment as well as its area. one may need the help of Matlab, or Mathematica or such tools.īut generally for each part you find its "I" about its own CG then add that to its area times the square of its CG height from xx axis. These can be broken into segments and small triangles on their sides. Now you subtract the "I" of two missing parts from the top and bottom. You find the "I" of a complete ring about xx axis first and that is done by calculating the "I" of the big circle: R = 0.625 subtracted by the "I" of small inner disk: R = 0.5.

$$I=\frac)$$Īssuming you want the moment of inertia, " $Ixx$", about the horizontal axis, you do as follows: You calculate the moment of inertia of the sector about the horizontal axis as follows: Your assembly consists of a small sector subtracted from a larger sector as shown below:
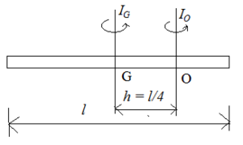
Since we have a compound object in both cases, we can use the parallel-axis theorem to find the moment of inertia about each axis. The radius of the sphere is 20.0 cm and has mass 1.0 kg. The rod has length 0.5 m and mass 2.0 kg. My first answer is kept below for reference. The moment of inertia of a disc of radius 0.5 m about its geometric axis is 2kg m2. Find the moment of inertia of the rod and solid sphere combination about the two axes as shown below. There seems to be a much easier way I overlooked, which I'll explain.


 0 kommentar(er)
0 kommentar(er)
